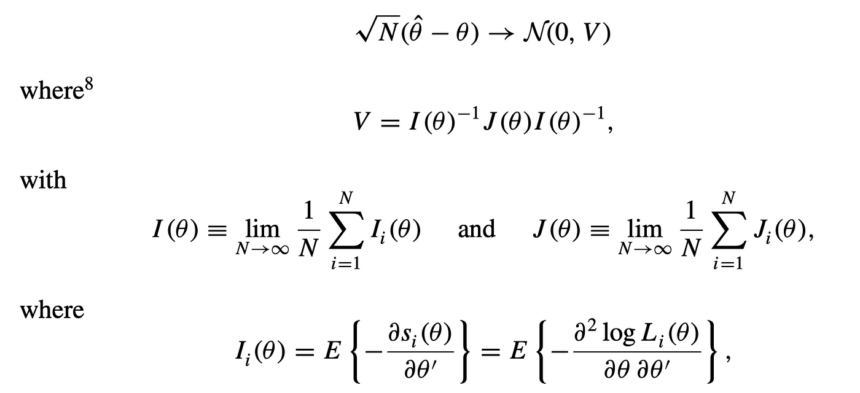Have you ever wondered how economists estimate complex models without relying on perfect data distributions? The generalized method of moments (GMM) is a powerful statistical technique that allows researchers to do just that. It’s a cornerstone of modern econometrics, providing a flexible framework for estimating parameters in models where the distribution of the data is unknown or difficult to characterize. So, let’s embark on a journey to understand what makes GMM so valuable and how it’s used in practice.
What is the Generalized Method of Moments?
The generalized method of moments is an estimation technique used in econometrics and statistics to estimate parameters in statistical models. It’s especially useful when you don’t have a complete understanding of the data’s distribution or when maximum likelihood estimation (MLE) is computationally infeasible. At its core, GMM is based on the idea that certain theoretical relationships, called moment conditions, should hold true in the population. These moment conditions essentially say that certain functions of the data, when averaged over the entire population, should equal zero (or some other known value).
Instead of trying to maximize a likelihood function (like in MLE), GMM focuses on minimizing the distance between the sample moments (calculated from your data) and the theoretical moments (implied by your model). In other words, we want to find the parameter values that make our model’s predictions as close as possible to what we observe in the real world, based on these pre-defined moment conditions.
Think of it like trying to find the perfect setting on a musical instrument. You know that when the instrument is tuned correctly, certain notes should resonate in a particular way. GMM is like adjusting the instrument’s settings (the parameters) until the observed resonances (sample moments) match the expected resonances (theoretical moments).
The Intuition Behind Moment Conditions
To truly grasp GMM, it’s crucial to understand moment conditions. These conditions are the heart and soul of the method. A moment condition is a mathematical statement that specifies a relationship between the parameters of the model and the data.
For example, let’s say we believe that the average height of adults in a population is 5’10”. This belief can be expressed as a moment condition: E[height – 5’10”] = 0, where E[] denotes the expected value. We expect the average of all the values to equate to zero.
In this case, the parameter we’re interested in is the average height. We would collect height data from a sample of adults, calculate the sample average, and then choose the parameter value (our estimate of the average height) that makes the sample moment as close to zero as possible.
The beauty of GMM is that you can use multiple moment conditions simultaneously. This allows you to incorporate various pieces of information about the data and the model into your estimation procedure. For example, in addition to knowing the average height, we might also know the variance of heights. We could then use both the mean and variance to estimate the distribution.
A common example from economics comes from the consumption-based asset pricing model. Here, a typical moment condition states that the expected value of the product of the pricing kernel (related to marginal utility of consumption) and the asset’s return, minus one, should be zero. This reflects the idea that, on average, investors should be fairly compensated for the risk they take when investing in an asset.
Reddit’s r/econometrics forums often discuss practical applications of moment conditions in various research settings, highlighting the importance of choosing relevant and informative conditions for effective estimation. The user ‘EconGeek42’ on Reddit mentioned, “The key to a good GMM is finding moment conditions that are both theoretically sound and empirically informative. Garbage in, garbage out, as they say.”
The GMM Estimator: Bridging Theory and Data
The GMM estimator is the mathematical formula used to find the parameter values that minimize the distance between the sample moments and the theoretical moments. The general form of the GMM estimator looks like this:
θ̂ = argmin (g(θ)’W g(θ))
Where:
- θ̂ is the GMM estimator (the estimated parameter values).
- g(θ) is a vector of sample moments. Each element of this vector represents the difference between a sample moment and its corresponding theoretical moment, evaluated at the parameter value θ.
- W is a weighting matrix. This matrix determines how much weight is given to each moment condition in the minimization process. A good choice of W can improve the efficiency of the GMM estimator.
The goal is to find the parameter values (θ̂) that make the expression g(θ)’W g(θ) as small as possible. In other words, we want to find the parameter values that make the sample moments as close as possible to the theoretical moments, taking into account the weights specified in the weighting matrix W.
The choice of the weighting matrix W is crucial. A common choice is to use the inverse of the sample covariance matrix of the moment conditions. This choice gives more weight to moment conditions that are estimated more precisely (i.e., have lower variance). This approach ensures that the estimation is efficient and provides more accurate results.
Advantages of GMM: Why It’s So Popular
GMM offers several advantages that make it a popular choice among economists and statisticians:
- Flexibility: It can be applied to a wide range of models, even when the distribution of the data is unknown. This is a major advantage over methods like maximum likelihood estimation, which require specific distributional assumptions.
- Robustness: It is robust to misspecification of the distribution. This means that even if your assumptions about the distribution of the data are slightly wrong, GMM can still provide reasonable estimates.
- Efficiency: With an optimal weighting matrix, GMM can be as efficient as maximum likelihood estimation when the distributional assumptions of MLE are correct.
- Overidentification Tests: GMM allows for overidentification tests, which can be used to check the validity of the model’s assumptions. If the model is overidentified (meaning that there are more moment conditions than parameters), we can test whether the moment conditions are consistent with the data. This can help us identify potential problems with our model.
These advantages make GMM a valuable tool for researchers working with complex and imperfect data.
Applications of GMM in Economics and Finance
GMM is widely used in various fields of economics and finance. Here are a few examples:
- Asset Pricing: GMM is used to estimate parameters in asset pricing models, such as the consumption-based capital asset pricing model (CCAPM). These models aim to explain the relationship between asset returns and macroeconomic variables like consumption and inflation.
- Macroeconomics: GMM is used to estimate parameters in dynamic stochastic general equilibrium (DSGE) models. These models are used to study the behavior of the economy as a whole and to analyze the effects of policy interventions.
- Microeconomics: GMM is used to estimate parameters in models of consumer behavior, firm behavior, and labor markets.
- Finance: In finance, GMM is used to estimate parameters in option pricing models, volatility models, and other financial models. It is also used for risk management and portfolio optimization.
These are just a few examples of the many applications of GMM. Its flexibility and robustness make it a valuable tool for researchers working on a wide range of problems.
As stated by Professor John Cochrane, a renowned economist at Stanford University, “GMM is a workhorse of empirical economics. Its flexibility allows us to confront theoretical models with real-world data, even when we don’t have perfect knowledge of the data’s underlying distribution.”
Challenges and Considerations in Using GMM
While GMM is a powerful tool, it’s not without its challenges. Here are a few things to keep in mind when using GMM:
- Choosing Moment Conditions: Selecting appropriate moment conditions is crucial. The moment conditions should be theoretically sound and empirically informative. Poorly chosen moment conditions can lead to biased or inefficient estimates.
- Choosing the Weighting Matrix: The choice of the weighting matrix can significantly affect the efficiency of the GMM estimator. While the optimal weighting matrix (the inverse of the sample covariance matrix of the moment conditions) is asymptotically efficient, it can perform poorly in small samples.
- Small Sample Bias: GMM estimators can be biased in small samples. This is because the sample moments may not be a good representation of the population moments.
- Weak Identification: If the moment conditions are weakly identified, the GMM estimator can be unstable and unreliable. This can happen when the moment conditions are not very sensitive to changes in the parameters.
Addressing these challenges requires careful consideration and a thorough understanding of the data and the model. Techniques like bootstrapping and bias correction can be used to mitigate the effects of small sample bias.
Step-by-Step Guide to Implementing GMM
Now, let’s walk through the steps of implementing generalized method of moments (GMM) in practice:
- Define Your Model: Start by clearly defining the model you want to estimate. This includes specifying the parameters you want to estimate and the theoretical relationships that you believe hold true.
- Choose Moment Conditions: Select a set of moment conditions that relate the parameters of your model to the data. These moment conditions should be based on your theoretical understanding of the model.
- Collect Data: Gather the data needed to calculate the sample moments. Make sure your data is of high quality and relevant to your model.
- Calculate Sample Moments: Calculate the sample moments from your data. These are the empirical counterparts of the theoretical moments.
- Choose a Weighting Matrix: Select a weighting matrix for the GMM estimator. A common choice is to use the inverse of the sample covariance matrix of the moment conditions.
- Minimize the GMM Objective Function: Use a numerical optimization algorithm to find the parameter values that minimize the GMM objective function. This involves finding the parameter values that make the sample moments as close as possible to the theoretical moments, taking into account the weighting matrix.
- Evaluate Your Results: Once you have estimated the parameters, evaluate your results. Check the statistical significance of the estimates and assess the goodness of fit of the model. You can also perform overidentification tests to check the validity of the model’s assumptions.
- Refine and Iterate: Based on your evaluation, refine your model and iterate on the estimation process. This may involve choosing different moment conditions, using a different weighting matrix, or addressing potential problems with the data.
This step-by-step guide provides a general framework for implementing GMM. The specific details will vary depending on the model and the data.
Conclusion: The Enduring Power of GMM
The generalized method of moments is a remarkably versatile and powerful tool in the econometrician’s arsenal. Its ability to estimate parameters without requiring strict distributional assumptions makes it invaluable for analyzing complex economic and financial models. While challenges exist in its implementation, a thorough understanding of its principles and careful attention to detail can unlock valuable insights. As economic models continue to evolve, GMM will undoubtedly remain a cornerstone of empirical research, helping us to better understand and navigate the complexities of the world around us. So, next time you encounter a research paper using GMM, you’ll have a deeper appreciation for the technique and its impact on our understanding of economic phenomena.
San Diego Workforce Partnership: Empowering Careers and Fueling the Local Economy